What Does the Band of Stability for Atomic Nuclei Refer to

xx.1 The Components of the Nucleus

Learning Objective

1. To sympathize the factors that impact nuclear stability.

Although most of the known elements have at least one isotope whose diminutive nucleus is stable indefinitely, all elements have isotopes that are unstable and disintegrate, or decay, at measurable rates by emitting radiation. Some elements take no stable isotopes and somewhen decay to other elements. In contrast to the chemic reactions that were the principal focus of before chapters and are due to changes in the arrangements of the valence electrons of atoms, the process of nuclear disuse results in changes inside an diminutive nucleus. We brainstorm our give-and-take of nuclear reactions by reviewing the conventions used to describe the components of the nucleus.

The Atomic Nucleus

As you learned in Affiliate i "Introduction to Chemistry", each chemical element can be represented by the annotation X Z A , where A, the mass number, is the sum of the number of protons and the number of neutrons, and Z, the atomic number, is the number of protons. The protons and neutrons that brand up the nucleus of an atom are called nucleonsThe protons and neutrons that make up the nucleus of an atom. , and an atom with a particular number of protons and neutrons is called a nuclideAn atom with a particular number of nucleons. . Nuclides with the same number of protons but different numbers of neutrons are chosen isotopes. Isotopes can also be represented by an culling note that uses the proper noun of the element followed by the mass number, such every bit carbon-12. The stable isotopes of oxygen, for example, tin be represented in whatsoever of the following ways:

X Z A : O 8 16 O eight 17 O 8 18 Ten A : O 16 O 17 O xviii element-A: oxygen-16 oxygen-17 oxygen-xviii

Because the number of neutrons is equal to A − Z, we encounter that the first isotope of oxygen has 8 neutrons, the second isotope nine neutrons, and the third isotope 10 neutrons. Isotopes of all naturally occurring elements on Earth are present in virtually fixed proportions, with each proportion constituting an isotope's natural abundance. For example, in a typical terrestrial sample of oxygen, 99.76% of the O atoms is oxygen-16, 0.xx% is oxygen-xviii, and 0.04% is oxygen-17.

Any nucleus that is unstable and decays spontaneously is said to exist radioactiveAny nucleus that is unstable and decays spontaneously, emitting particles and electromagnetic radiations. , emitting subatomic particles and electromagnetic radiation. The emissions are collectively called radioactivity and can be measured. Isotopes that emit radiation are called radioisotopesAn isotope that emits radiations. . Equally you learned in Affiliate 14 "Chemical Kinetics", the rate at which radioactive decay occurs is feature of the isotope and is generally reported as a one-half-life (t _1/2), the amount of fourth dimension required for half of the initial number of nuclei present to decay in a first-social club reaction. (For more information on half-life, see Chapter xiv "Chemical Kinetics", Section 14.five "Half-Lives and Radioactive decay Kinetics".) An isotope's half-life can range from fractions of a 2nd to billions of years and, among other applications, tin be used to measure the age of aboriginal objects. Example 1 and its corresponding do review the calculations involving radioactive disuse rates and one-half-lives.

Example 1

Fort Rock Cave in Oregon is the site where archaeologists discovered several Indian sandals, the oldest ever plant in Oregon. Analysis of the ¹⁴C content of the sagebrush used to make the sandals gave an average decay charge per unit of 5.one disintegrations per minute (dpm) per gram of carbon. The current ¹⁴C/¹²C ratio in living organisms is ane.three × 10⁻¹², with a decay rate of 15 dpm/g C. How long ago was the sagebrush in the sandals cutting? The one-half-life of ¹⁴C is 5730 yr.

Given: radioisotope, electric current ¹⁴C/¹²C ratio, initial decay charge per unit, terminal disuse charge per unit, and one-half-life

Asked for: age

Strategy:

A Apply Equation 14.xxx to summate N ₀/North, the ratio of the number of atoms of ^fourteenC originally nowadays in the sample to the number of atoms now nowadays.

B Substitute the value for the one-half-life of ¹⁴C into Equation 14.28 to obtain the rate constant for the reaction.

C Substitute the calculated values for N ₀/Due north and the rate constant into Equation 14.32 to obtain the elapsed time t.

Solution:

We can use the integrated rate constabulary for a first-social club nuclear reaction (Equation 14.32) to calculate the amount of time that has passed since the sagebrush was cut to make the sandals:

ln N N 0 = − k t

A From Equation 14.30, we know that A = kN. We tin therefore use the initial and concluding activities (A ₀ = 15 and A = 5.1) to calculate N ₀/N:

A 0 A = m N 0 k N = N 0 North = fifteen 5.1

B At present we can calculate the charge per unit constant k from the half-life of the reaction (5730 yr) using Equation xiv.28:

t 1 / 2 = 0.693 k

Rearranging this equation to solve for k,

k = 0.693 t one / 2 = 0.693 5730 yr = 1.21 × 10 − 4 yr − one

C Substituting the calculated values into the equation for t,

t = ln ( N 0 / Northward ) k = ln ( 15 / 5.ane ) 1.21 × 10 − 4 yr − one = 8900 twelvemonth

Thus the sagebrush in the sandals is nearly 8900 yr erstwhile.

Exercise

While trying to find a suitable way to protect his own burying chamber, the aboriginal Egyptian pharaoh Sneferu developed the pyramid, a burying structure that protected desert graves from thieves and exposure to wind. Analysis of the ¹⁴C content of several items in pyramids built during his reign gave an boilerplate decay charge per unit of eight.6 dpm/thousand C. When were the objects in the bedchamber created?

Answer: about 4600 twelvemonth ago, or virtually 2600 BC

Nuclear Stability

Every bit discussed in Chapter 1 "Introduction to Chemical science", the nucleus of an atom occupies a tiny fraction of the volume of an atom and contains the number of protons and neutrons that is characteristic of a given isotope. Electrostatic repulsions would usually cause the positively charged protons to repel each other, but the nucleus does not fly autonomously because of the strong nuclear forceAn extremely powerful only very short-range attractive force betwixt nucleons that keeps the nucleus of an cantlet from flying autonomously (due to electrostatic repulsions between protons). , an extremely powerful but very short-range attractive force between nucleons (Figure 20.i "Competing Interactions within the Atomic Nucleus"). All stable nuclei except the hydrogen-ane nucleus (^oneH) contain at to the lowest degree one neutron to overcome the electrostatic repulsion betwixt protons. Equally the number of protons in the nucleus increases, the number of neutrons needed for a stable nucleus increases fifty-fifty more than rapidly. As well many protons (or too few neutrons) in the nucleus result in an imbalance between forces, which leads to nuclear instability.

Figure xx.one Competing Interactions within the Atomic Nucleus

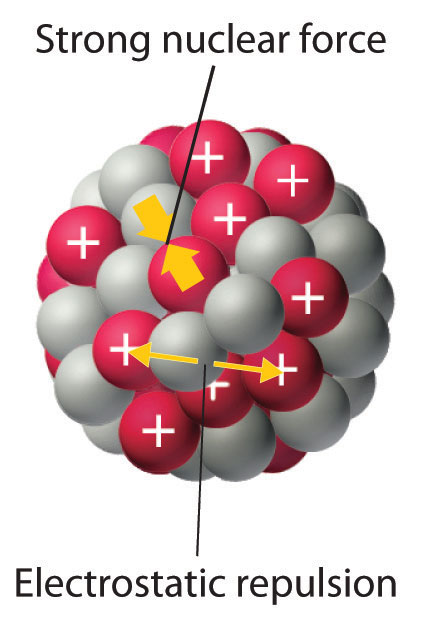
Electrostatic repulsions between positively charged protons would normally cause the nuclei of atoms (except H) to wing autonomously. In stable diminutive nuclei, these repulsions are overcome past the potent nuclear force, a short-range but powerful bonny interaction betwixt nucleons. If the attractive interactions due to the strong nuclear force are weaker than the electrostatic repulsions between protons, the nucleus is unstable, and it volition eventually decay.

The human relationship between the number of protons and the number of neutrons in stable nuclei, arbitrarily defined as having a half-life longer than 10 times the age of Earth, is shown graphically in Figure xx.two "The Human relationship betwixt Nuclear Stability and the Neutron-to-Proton Ratio". The stable isotopes course a "peninsula of stability" in a "sea of instability." Only two stable isotopes, ¹H and ^threeHe, have a neutron-to-proton ratio less than ane. Several stable isotopes of light atoms have a neutron-to-proton ratio equal to ane (e.g., H 2 4 eastward, B 5 10 , and C xx 40 a ). All other stable nuclei have a higher neutron-to-proton ratio, which increases steadily to nigh ane.5 for the heaviest nuclei. Regardless of the number of neutrons, however, all elements with Z > 83 are unstable and radioactive.

Effigy 20.2 The Relationship between Nuclear Stability and the Neutron-to-Proton Ratio

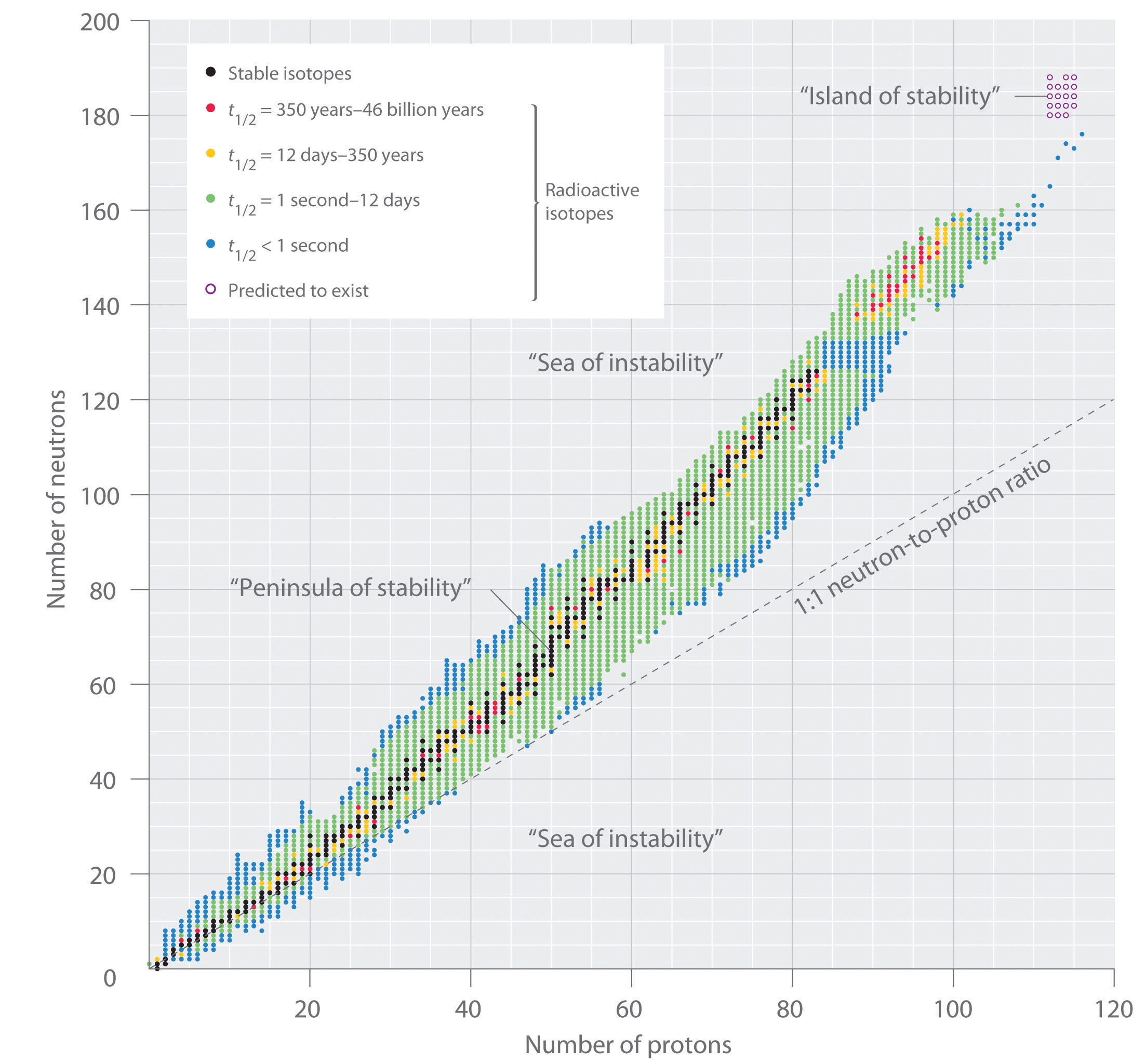
In this plot of the number of neutrons versus the number of protons, each blackness point corresponds to a stable nucleus. In this nomenclature, a stable nucleus is arbitrarily defined as one with a half-life longer than 46 billion years (x times the age of Earth). As the number of protons (the atomic number) increases, the number of neutrons required for a stable nucleus increases even more than rapidly. Isotopes shown in red, yellow, greenish, and bluish are progressively less stable and more radioactive; the further an isotope is from the diagonal band of stable isotopes, the shorter its half-life. The royal dots signal superheavy nuclei that are predicted to exist relatively stable, meaning that they are expected to be radioactive merely to have relatively long half-lives. In almost cases, these elements have not yet been observed or synthesized.

Data source: National Nuclear Data Center, Brookhaven National Laboratory, Evaluated Nuclear Structure Data File (ENSDF), Chart of Nuclides, http://world wide web.nndc.bnl.gov/nautical chart.

As shown in Figure 20.3 "The Relationship between the Number of Protons and the Number of Neutrons and Nuclear Stability", more than one-half of the stable nuclei (166 out of 279) have even numbers of both neutrons and protons; only six of the 279 stable nuclei do non have odd numbers of both. Moreover, certain numbers of neutrons or protons consequence in especially stable nuclei; these are the then-called magic numbers 2, viii, xx, 50, 82, and 126. For instance, tin can (Z = l) has 10 stable isotopes, but the elements on either side of tin in the periodic tabular array, indium (Z = 49) and antimony (Z = 51), have just 2 stable isotopes each. Nuclei with magic numbers of both protons and neutrons are said to be "doubly magic" and are even more than stable. Examples of elements with doubly magic nuclei are H ii iv e, with two protons and two neutrons, and P 82 208 b, with 82 protons and 126 neutrons, which is the heaviest known stable isotope of any element.

Effigy 20.3 The Relationship between the Number of Protons and the Number of Neutrons and Nuclear Stability

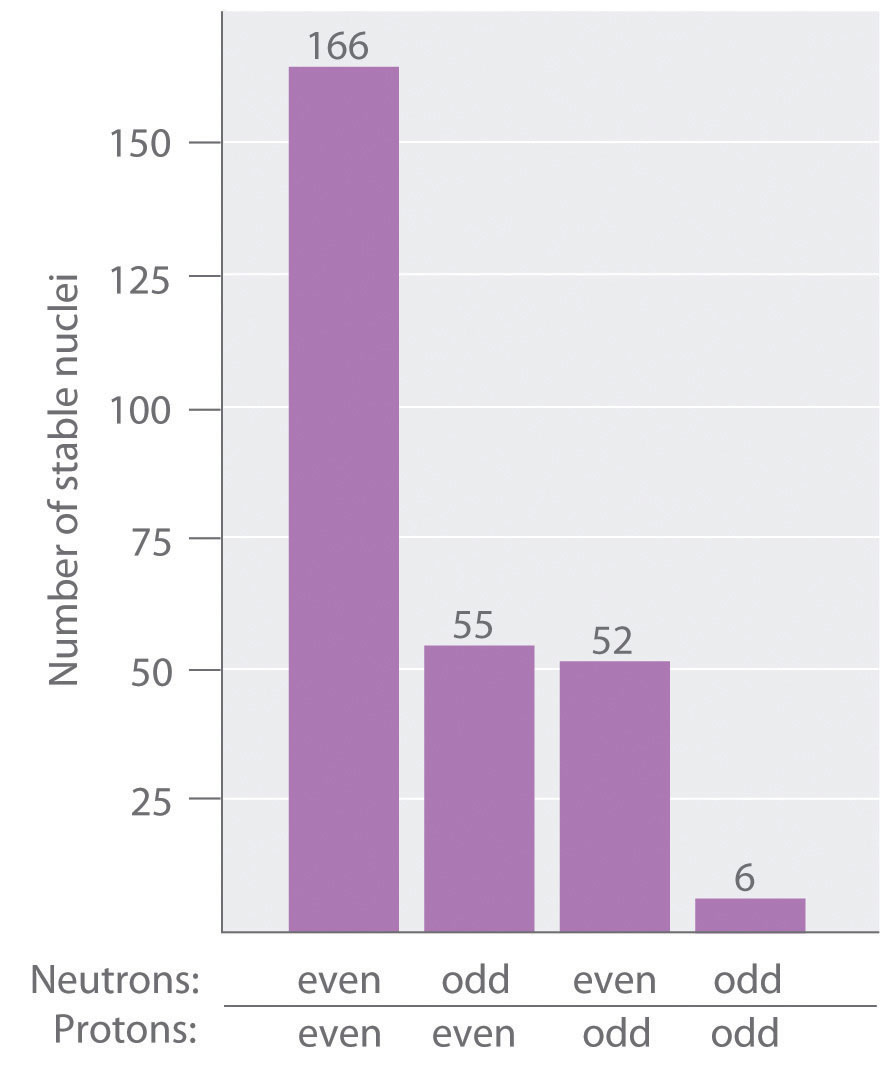
Most stable nuclei comprise even numbers of both neutrons and protons.

The pattern of stability suggested by the magic numbers of nucleons is reminiscent of the stability associated with the closed-shell electron configurations of the noble gases in group 18 and has led to the hypothesis that the nucleus contains shells of nucleons that are in some ways analogous to the shells occupied by electrons in an atom. Every bit shown in Figure 20.2 "The Human relationship between Nuclear Stability and the Neutron-to-Proton Ratio", the "peninsula" of stable isotopes is surrounded by a "reef" of radioactive isotopes, which are stable enough to be for varying lengths of time before they somewhen disuse to produce other nuclei.

Example two

Classify each nuclide as stable or radioactive.

1. P 15 30
2. T 43 98 c
3. tin-118
4. P 94 239 u

Given: mass number and diminutive number

Asked for: predicted nuclear stability

Strategy:

Use the number of protons, the neutron-to-proton ratio, and the presence of fifty-fifty or odd numbers of neutrons and protons to predict the stability or radioactivity of each nuclide.

Solution:

1. This isotope of phosphorus has 15 neutrons and xv protons, giving a neutron-to-proton ratio of 1.0. Although the atomic number, fifteen, is much less than the value of 83 higher up which all nuclides are unstable, the neutron-to-proton ratio is less than that expected for stability for an chemical element with this mass. As shown in Figure twenty.2 "The Relationship between Nuclear Stability and the Neutron-to-Proton Ratio", its neutron-to-proton ratio should exist greater than ane. Moreover, this isotope has an odd number of both neutrons and protons, which likewise tends to brand a nuclide unstable. Consequently, P xv xxx is predicted to be radioactive, and it is.
2. This isotope of technetium has 55 neutrons and 43 protons, giving a neutron-to-proton ratio of 1.28, which places T 43 98 c near the edge of the ring of stability. The atomic number, 55, is much less than the value of 83 in a higher place which all isotopes are unstable. These facts suggest that T 43 98 c might be stable. However, T 43 98 c has an odd number of both neutrons and protons, a combination that seldom gives a stable nucleus. Consequently, T 43 98 c is predicted to be radioactive, and it is.
3. Can-118 has 68 neutrons and l protons, for a neutron-to-proton ratio of 1.36. As in part b, this value and the atomic number both suggest stability. In addition, the isotope has an even number of both neutrons and protons, which tends to increase nuclear stability. Most important, the nucleus has 50 protons, and fifty is one of the magic numbers associated with particularly stable nuclei. Thus Southward 50 118 north should be particularly stable.
4. This nuclide has an atomic number of 94. Because all nuclei with Z > 83 are unstable, P 94 239 u must be radioactive.

Exercise

Classify each nuclide as stable or radioactive.

1. T 90 232 h
2. C 20 forty a
3. O eight 15
4. 50 57 139 a

Answer:

1. radioactive
2. stable
3. radioactive
4. stable

Superheavy Elements

In addition to the "peninsula of stability," Figure 20.2 "The Relationship between Nuclear Stability and the Neutron-to-Proton Ratio" shows a small "isle of stability" that is predicted to be in the upper right corner. This isle corresponds to the superheavy elementsAn element with an diminutive number near the magic number of 126. , with atomic numbers near the magic number 126. Because the next magic number for neutrons should be 184, it was suggested that an element with 114 protons and 184 neutrons might be stable enough to be in nature. Although these claims were met with skepticism for many years, since 1999 a few atoms of isotopes with Z = 114 and Z = 116 accept been prepared and found to be surprisingly stable. One isotope of element 114 lasts 2.vii seconds before decaying, described as an "eternity" by nuclear chemists. Moreover, at that place is recent evidence for the existence of a nucleus with A = 292 that was found in ²³²Th. With an estimated half-life greater than ten⁸ years, the isotope is particularly stable. Its measured mass is consistent with predictions for the mass of an isotope with Z = 122. Thus a number of relatively long-lived nuclei may well exist attainable amid the superheavy elements.

Summary

Subatomic particles of the nucleus (protons and neutrons) are called nucleons. A nuclide is an atom with a particular number of protons and neutrons. An unstable nucleus that decays spontaneously is radioactive, and its emissions are collectively called radioactivity. Isotopes that emit radiation are called radioisotopes. Each nucleon is attracted to other nucleons past the strong nuclear force. Stable nuclei generally have even numbers of both protons and neutrons and a neutron-to-proton ratio of at to the lowest degree 1. Nuclei that contain magic numbers of protons and neutrons are often especially stable. Superheavy elements, with atomic numbers nearly 126, may fifty-fifty be stable enough to be in nature.

Key Takeaway

• Nuclei with magic numbers of neutrons or protons are peculiarly stable, every bit are those nuclei that are doubly magic.

Conceptual Problems

1. What distinguishes a nuclear reaction from a chemical reaction? Apply an instance of each to illustrate the differences.

2. What do chemists mean when they say a substance is radioactive?

3. What characterizes an isotope? How is the mass of an isotope of an chemical element related to the atomic mass of the element shown in the periodic table?

4. In a typical nucleus, why does electrostatic repulsion between protons not destabilize the nucleus? How does the neutron-to-proton ratio affect the stability of an isotope? Why are all isotopes with Z > 83 unstable?

5. What is the significance of a magic number of protons or neutrons? What is the relationship between the number of stable isotopes of an element and whether the element has a magic number of protons?

6. Do you look Bi to have a big number of stable isotopes? Ca? Explain your answers.

7. Potassium has iii common isotopes, ³⁹Thousand, ^twoscoreThousand, and ⁴¹Grand, but only potassium-40 is radioactive (a beta emitter). Advise a reason for the instability of ⁴⁰G.

8. Samarium has 11 relatively stable isotopes, but only 4 are nonradioactive. One of these 4 isotopes is ¹⁴⁴Sm, which has a lower neutron-to-proton ratio than lighter, radioactive isotopes of samarium. Why is ¹⁴⁴Sm more stable?

Answers

5. Isotopes with magic numbers of protons and/or neutrons tend to be especially stable. Elements with magic numbers of protons tend to have more than stable isotopes than elements that exercise not.

7. Potassium-40 has 19 protons and 21 neutrons. Nuclei with odd numbers of both protons and neutrons tend to exist unstable. In improver, the neutron-to-proton ratio is very depression for an element with this mass, which decreases nuclear stability.

Numerical Problems

1. Write the nuclear symbol for each isotope using X Z A note.

   1. chlorine-39
   2. lithium-8
   3. osmium-183
   4. zinc-71

2. Write the nuclear symbol for each isotope using X Z A notation.

   1. pb-212
   2. helium-v
   3. oxygen-19
   4. plutonium-242

3. Requite the number of protons, the number of neutrons, and the neutron-to-proton ratio for each isotope.

   1. iron-57
   2. ¹⁸⁵W
   3. potassium-39
   4. ¹³¹Xe

4. Give the number of protons, the number of neutrons, and the neutron-to-proton ratio for each isotope.

   1. technetium-99m
   2. ¹⁴⁰La
   3. radium-227
   4. ²⁰⁸Bi

5. Which of these nuclides practise you await to be radioactive? Explain your reasoning.

   1. ^twentyNe
   2. tungsten-184
   3. ¹⁰⁶Ti

6. Which of these nuclides practice you await to exist radioactive? Explain your reasoning.

   1. ¹⁰⁷Ag
   2. ⁵⁰Five
   3. lutetium-176

Answers

1. 1. C 17 39 l
   2. L three 8 i
   3. O 76 183 s
   4. Z 30 71 due north
3. 1. 26 protons; 31 neutrons; 1.19
   2. 74 protons; 111 neutrons; 1.fifty
   3. 19 protons; 20 neutrons; i.05
   4. 54 protons; 77 neutrons; 1.43

huffmanwitena.blogspot.com

Source: https://saylordotorg.github.io/text_general-chemistry-principles-patterns-and-applications-v1.0/s24-01-the-components-of-the-nucleus.html

Share this post